iPotrubí.cz

 Zákonitostmi mechaniky tekutin (hydromechanika a aeromechanika) se řídí proudící tekutiny v potrubí. Z těchto zákonitostí se dají odvodit síly, které potrubí zatěžují. Z těcho důvodů se mechanice tekutin věnuje tato kapitola specifikující zatížení od proudění tekutiny na potrubí.

Vedle rovnice kontinuity a Bernoulliho rovnice, lze ještě určit rovnici o změně hybnosti tekutiny, tj. impulsovou větou. Je zde uvedena proto, že sleduje výsledný silový účinek tekutiny na stěnu potrubní komponenty. Tento silový účinek je zatěžovací síla při pevnostním výpočtu potrubí.

Odvození impulsové věty je následující: Změna hybnosti je dána impulsu síly, což je dáno z mechaniky. Pro konstantní sílu F a hmotnost m  se dostane po integraci:

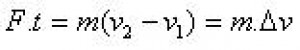
 Úpravou této rovnice - dělením t - se získá:

která slouží k výpočtu sil, kterými působí obtékané plochy na proud kapaliny. Součin

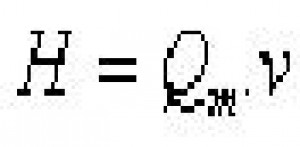
je průtoková hybnost. Síla F vyvolaná proudící kapalinou je rovna změně průtokové hybnosti:

F=H₂-H₁

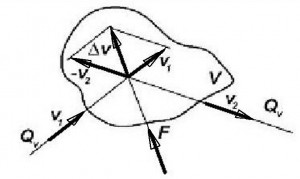
Obrázek  Znázornění impulzové věty

Nyní se vraťme k rovnici kontinuity. Rovnice kontinuity je rovnice, která platí pro ustálené proudění ideální kapaliny v uzavřené trubici a popisuje vztah mezi rychlostí proudění v a obsahem průřezu S v jednom místě trubice:

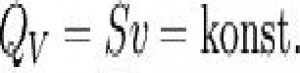
Z rovnice kontinuity plyne:

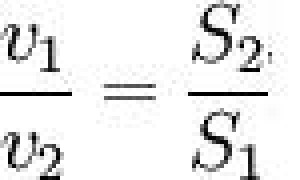
neboli poměr rychlostí v₁ a v₂ proudění ve dvou místech je převrácený k poměru obsahů průřezů S₁ a S₂ trubice v těchto místech. Čím užší trubice, tím rychlejší proudění.

        Platnost rovnice kontinuity vychází ze zachování stejného objemového průtoku ve všech místech trubice (za podmínky ustáleného proudění ideální kapaliny v uzavřené trubici).

Tyto vztahy lze zobecnit i pro stlačitelné kapaliny. Pro stlačitelné kapaliny se mění hustota a proto se nezachovává objemový tok. Veličina která se zachováva je hmotnostní tok. Rovnici kontinuity lze pak zapsat jako

,

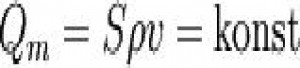což znamená, že při ustáleném proudění stlačitelné kapaliny je hmotnostní tok kapaliny v libovolném kolmém průřezu proudové trubice konstantní.

            Dále se také vraťme k Bernoulliově rovnici, konkrétně ke vztahu rychlost proudění – tlak. Bernoulliho rovnice je vztah užívaný v mechanice tekutin, který odvodil Daniel Bernoulli a který vyjadřuje zákon zachování mechanické energie pro ustálené proudění ideální kapaliny. (Energie je v rovnici přepočtena na objemovou jednotku kapaliny.)

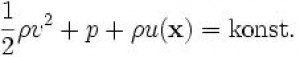
kde   u   je potenciál vnějšího konzervativního pole mechanické síly (gravitační síly, unášivé setrvačné síly nebo jejich kombinace jako je tíhová síla) v daném bodě.

První člen v Bernoulliho rovnici představuje kinetickou energii, druhý člen představuje tlakovou potenciální energii objemové jednotky kapaliny a třetí člen potenciální energii objemové jednotky kapaliny v silovém poli vnější konzervativní mechanické síly, v němž se kapalina nachází. Součet kinetické energie a potenciální energie (tlakové + vnější) je ve všech místech trubice stejný. Tato rovnice bývá často uváděna ve tvaru, který platí pro tíhové či homogenní gravitační pole:

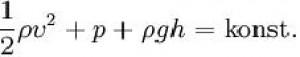
           Platí, že pokud na kapalinu v klidu působí tíhová síla, je ve stejné hloubce v každém bodě stejný tlak. Pokud je kapalina v pohybu tak tento vztah neplatí. Slovy můžeme Bernoulliho jev popsat takto: v místě s větším průřezem má proudící kapalina větší tlak, ale menší rychlost, zatímco v místě s menším obsahem průřezu má menší tlak, ale větší rychlost. (Fakt, že při větším průřezu je rychlost kapaliny menší je důsledkem rovnice kontinuity.)

3. Reakce od proudění tekutiny v redukci

Redukce – kuželové potrubí, kde proudění tekutiny je ve směru rozšiřujícího se průřezu – se nazývá difuzor. A jestliže je proudění kapaliny ve směru zužujícího se průřezu, redukce se nazývá konfuzor.

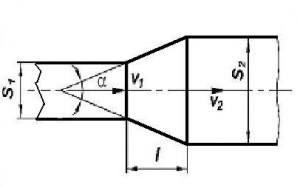
Obrázek Proudění v rozšíření

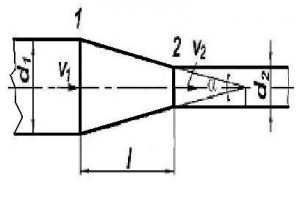
Obrázek Proudění v redukci

Odvození síly: Množství kapaliny je v průřezu S₁ a S₂ stejné, tj. aplikace rovnice kontinuity. Z toho vyplývá i změna rychlosti. A právě změnou rychlosti je určena síla působící na redukci. Platí toto:

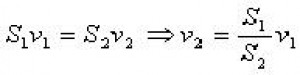
 Z impulzové věty odvodíme

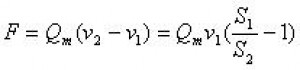
        Dále zde působí síla rozdílu tlaků, neboť z Bernoulliovy rovnice platí, že při rychlejší kapalině je menší tlak a naopak. Tento rozdíl tlaků působí na plochu mezikruží tvořenou oběma průměry potrubí. Součet obou těchto sil je vždy konstantní a namáhá potrubí v osovém směru. Výsledná síla tedy nemusí záviset na rychlosti proudění.

4. Reakce od proudění tekutiny v oblouku

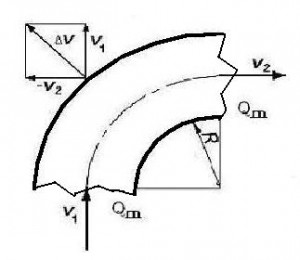
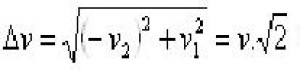
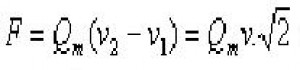
5. Sčítání sil od proudění v reálném potrubí

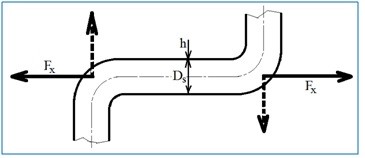
         Sčítáme-li reakce od ustáleného proudění v potrubí v případech předchozích dvou kapitol, zjistíme, že se vždy dvě a dvě ruší. Jako příklad si dáme za sebou dva oblouky a vypočítáme si, jak namáhají potrubí.

Síla F_x namáhá tedy potrubí mezi nimi na tah. Snadno si tedy vypočítáme napětí, které způsobuje ustálené proudění v potrubí. Zjistíme si, že vyjde vzorec o zatížení tlakem pro osové membránové napětí.

Odčítání a vzájemné rušení těchto reakcí se přerušují např. v případech, které jsou uvedeny dále. Tyto případy musíme při výpočtu potrubí zapracovat.