3. Místní tlakové ztráty
1. Použité značky a jednotky
|
Poř. č. |
Značka |
Název veličiny |
|
1. |
D[m] |
vnitřní průměr potrubí, vnitřní průměr vstupu a výstupu armatury |
|
2. |
D1, D2[m] |
vnitřní průměr potrubí před změnou a po změně |
|
3. |
S1, S2 [m2] |
průtočný průřez před změnou a po změně |
|
4. |
r[m] |
poloměr kolena, poloměr zaoblené hrany |
|
5. |
Δp[Pa] |
místní tlaková ztráta (s různými indexy) |
|
6. |
Q[m3·s-1] |
objemový průtok |
|
7. |
ρ[kg·m-3] |
hustota proudícího média |
|
8. |
KVS |
jmenovitý průtokový součinitel |
|
9. |
w [m·s-1] |
střední rychlost proudění |
|
10. |
ζ [-] |
ztrátový součinitel (s různými indexy) |
|
11. |
ε [-] |
pomocná veličina pro výpočet ztrátového součinitele |
|
12. |
Z [m] |
pokles celkové měrné energie proudění (s různými indexy) |
|
13. |
δ[-] |
úhel změny tvarovky |
|
14. |
g[m·s-2] |
gravitační zrychlení |
|
15. |
|
|
|
16. |
|
|
2. Místní ztráty
Potrubní větev nebývá přímočará a může být tvořena dalšími potrubními prvky (odbočky různých tvarů, oblouky, redukce), armaturami, filtry, měřidly a dalšími průtočnými částmi. V těchto částech potrubních tras vzniká tlaková ztráta podobně jako v přímém potrubí. Tyto tlakové ztráty bývají mnohem intenzivnější než na rovném úseku potrubí vzhledem k tomu, že při průtoku těmito částmi dochází i ke změně tvaru průtočného trubky, směru proudění a často i ke škrcení. Z pohledu tlakové ztráty se tyto prvky nazývají místní ztráty. Místní ztráta se vypočítá podle podobných vztahů, jako tlaková ztráta rovného úseku potrubí. Z uvedených vztahů, lze odvodit vztah pro výpočet tlakové ztráty:
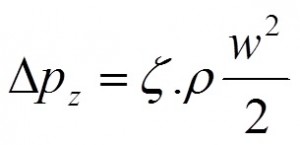
Anebo ztráty měrné energie
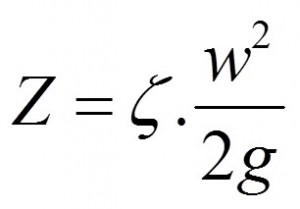
Z uvedeného je vidět, že v dalším budeme hledat, jak co nejjednodušeji získat ztrátový součinitel potrubí ζ .
2.1. Místní ztráty v tvarovkách
U jednoduchých potrubních prvků lze jejich ztrátový součinitel ζ i vypočítat, častěji se ale vychází z měření. Příslušný ztrátový součinitel poskytuje výrobce daného potrubního prvku popřípadě, dovoluje–li to požadovaná přesnost výpočtu, lze vycházet z tabulek. Za speciální případ místního odporu, lze považovat i vstupy a výstupy z trubky. Na okrajích je totiž proudění většinou neustálené a ovlivněné tvarem začátku či konce potrubí.
2.1.1. Místní ztráta při vtoku do potrubí
|
Typ vtoku – vstupní hrany |
Platnost |
Ztrátový součinitel |
|
Potrubí zasahuje do nádrže |
|
0,8 – 1,0 |
|
Ostrá hrana |
|
0,5 |
|
Sražená hrana |
0,1D |
0,25 |
|
Zaoblená hrana |
|
0,2 |
|
Sražená hrana |
0,2D – 0,3D 40 – 80° |
0,13 |
|
Kruhově zaoblená hrana |
r=0,2D |
0,11 |
|
Strofoidický vtok (dle Lískovce) |
|
0,04 |
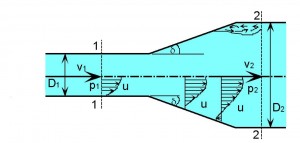
Tuto ztrátu lze teoreticky odvodit na základě věty o hybnosti a Bernoulliho rovnive. Musí však platit předpoklad, že tlak v potrubí před rozšířením je stejný jako tla v potrubí těsně za rozšířením. Tímto odvozením dostaneme vzorec pro výpočet hodnoty součinitele místní ztráty náhlého rozšíření:
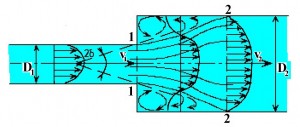
Obr. Náhlé rozšíření potrubí
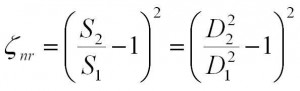
Tyto hodnoty dále zpracujeme do tabulky:
|
D2/D1 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
3,0 |
|
S2/S1 |
1,0 |
1,44 |
1,96 |
2,56 |
3,24 |
4,0 |
9,0 |
|
Ztrátový součinitel |
0,0 |
0,194 |
0,922 |
2,434 |
5,018 |
9,0 |
64,0 |
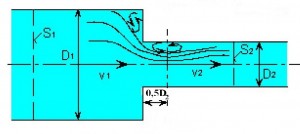
Obr. Náhlé zúžení potrubí
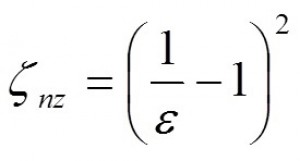
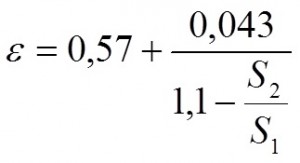
|
D2/D1 |
0,95 |
0,89 |
0,83 |
0,775 |
0,71 |
0,63 |
0,55 |
0,45 |
0,32 |
|
S2/S1 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
0,3 |
0,2 |
0,1 |
|
Ztrátový součinitel |
0,075 |
0,16 |
0,23 |
0,275 |
0,31 |
0,34 |
0,36 |
0,38 |
0,4 |
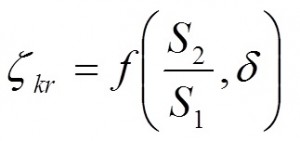
|
S2/S1 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
6,0 |
8,0 |
|
2.δ=5° |
0,03 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,10 |
|
2.δ=10° |
0,02 |
0,05 |
0,06 |
0,07 |
0,08 |
0,10 |
0,12 |
|
2.δ=15° |
|
0,06 |
0,08 |
0,10 |
0,13 |
0,17 |
0,20 |
|
2.δ=20° |
|
|
|
|
0,17 |
0,20 |
0,23 |
b) Kónické zúžení (redukce)
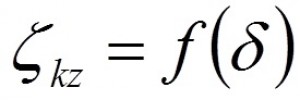
|
2.δ |
5° |
7° |
10° |
20° |
30° |
60° |
|
Ztrátový součinitel |
0,06 |
0,12 |
0,16 |
0,20 |
0,24 |
0,32 |
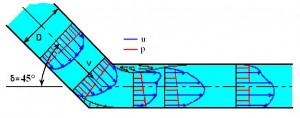
Obr. Ostrá změna směru proudění
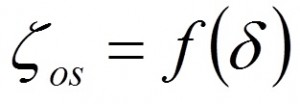
|
δ |
15° |
30° |
45° |
60° |
90° |
|
Ztrátový součinitel – hladká potrubí |
0,04 |
0,13 |
0,24 |
0,47 |
1,13 |
|
Ztrátový součinitel – drsná potrubí |
0,06 |
0,17 |
0,32 |
0,68 |
1,27 |
b) Obloukové koleno
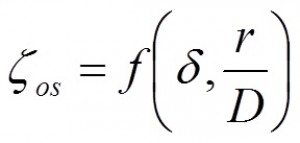
Dále budou v tabulce uvedeny ztrátové součinitele pro obloukové koleno devadesátistupňové.
|
r/D |
1,0 |
1,5 |
2,0 |
4,0 |
6,0 |
10,0 |
20,0 |
|
Ztrátový součinitel – hladká potrubí |
0,21 |
0,17 |
0,15 |
0,11 |
0,09 |
0,07 |
0,05 |
|
Ztrátový součinitel – drsná potrubí |
0,42 |
0,34 |
0,30 |
0,22 |
0,18 |
0,14 |
0,10 |
2.2. Místní ztráty v armaturách
V případě armatur obvykle výrobce dodává grafy závislosti její tlakové ztráty na průtoku (podle druhu protékajícího média). Pokud je znám jmenovitý průtokový součinitel armatury KVS lze ztrátu v závislosti na průtoku vypočítat z uvedené definice. Popřípadě je možné odvodit ze zmíněné definice přímo ztrátový součinitel armatury:
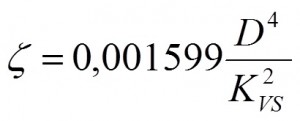
Vztah je odvozen pro průtok vody. Jmenovitý průtokový součinitel se měří na úseku 2D před armaturou a 8D za armaturou, proto takto vypočítaný ztrátový součinitel zahrnuje i tuto délku potrubí. Takže skutečný ztrátový součinitel armatury je nižší o ztrátový součinitel odpovídající 10D hladkého potrubí.
Při výběru nejvhodnější uzavírací armatury se nejdříve stanoví povolená tlaková ztráta Δpz při objemovém průtoku Q a hustotě proudícího média ρ1. Vypočítá se jmenovitý průtokový součinitel KVS. Dále se z katalogu armatur příslušného výrobce vybere armatura s nejbližším vyšším KVS. Existují i jiné typy součinitelů, zpravidla odvozené od tlakové ztráty armatury. Záleží na výrobci, jakou metodiku porovnávání armatur zvolí.
3. Literatura a odkazy pro další a podrobnější informace
Steidl H., Neužil L., Fořt I., Vlček J.: Úvod do proudění tekutin a sdílení tepla, Academia Praha, 1975
http://www.transformacni-technologie.cz/vznik-tlakove-ztraty-pri-proudeni-tekutiny.html
http://www.tzb-info.cz/1002-priblizny-vypocet-tlakove-ztraty-trenim-v-potrubi
http://vytapeni.tzb-info.cz/tabulky-a-vypocty/87-vypocet-tlakove-ztraty-trenim-v-potrubi
http://www.qpro.cz/Ztraty-trenim-ve-vzduchotechnickem-potrubi