Příspěvek - Bourdonův jev pro potrubí
18. 9. 2013
1. Prodlužování přímého potrubí způsobeného vnitřním tlakem
V reálném potrubí je tendence k prodloužení u trubek a k deformacím kolen a oblouků vlivem vnitřního tlaku. Uvedené se nazývá Bourdonův jev.
Vypočítáme tedy poměrnou změnu objemu od osového napětí sigma 1 v potrubí: Tato poměrná změna je reprezentována především poměrnou změnou délky, neboť ostatní dvě poměrné změny jsou vůči délce zanedbatelné. Máme zde rovinnou napjatost, proto:
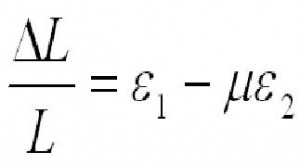
kde epsilon1 je poměrné osové prodloužení
epsilon2 je poměrné obvodové prodloužení
mí je Poissonovo číslo
Z Hookova zákona platí:
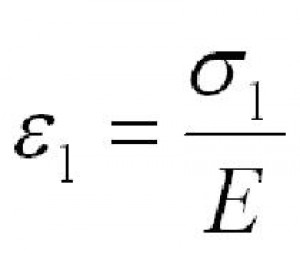
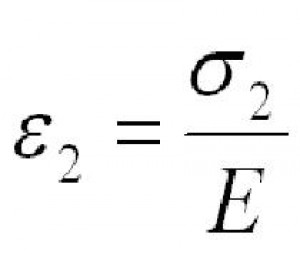
Pro osové napětí potrubí platí již dříve odvozený vztah:
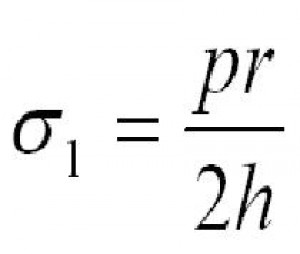
a dále pro obvodové napětí potrubí platí již dříve odvozený vztah:
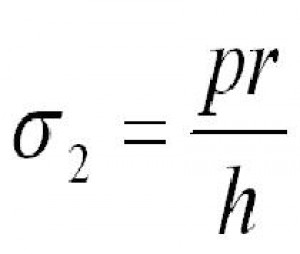
A pro prodloužení trubky je možno odvodit následující vzorec:
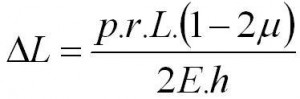
kde delta L je prodloužení potrubí vlivem vnitřního tlaku
p vnitřní tlak
r střední poloměr potrubí
L původní délka potrubí
mí Poissonovo číslo
E modul pružnosti
h tloušťka stěny potrubí
2. Deformace oblouků způsobená vnitřním tlakem
Jde tedy o Bourdonův jev v obloucích potrubí . Podobně jako Bourdonův jev v obloucích, funguje „Bourdonova trubice“ v tlakoměrech, neboť trubice má tvar oblouku. Deformace tohoto oblouku, v kterém je meřený tlak, se převádí mechanickým převodem na ručičku se stupnicí.
Princip Bourdonova jevu spočívá v tom, že je osové napětí v anuloidu na vnitřní straně větší než na vnější. Uvedené vyplývá z aplikace Laplaceovy rovnice na anuloid. Jestliže anuloid při zachování vnitřního tlaku rozřízneme a vyrobíme z něj např. čtyři kolena, pak tato napětí uvolníme a oblouk se deformuje („narovná“).
Jestliže vypočítáme prodloužení od vnitřního tlaku zvlášť pro vnitřní a zvlášť pro vnější stranu oblouku, a to podobně, jako jsme to udělali v přechozí kapitole, získáme deformaci vniřní a vnější strany. Z tohoto rozdílu se může vypočítat úhel natočení („narovnání“) kolena či oblouku. Toto je však velmi přibližná úvaha.
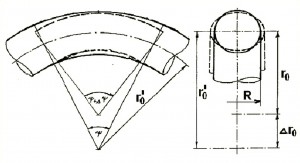
Obr. deformace kolena
Dále nesmíme zapomenout, že při působení zatížení od vnějšího tlaku (Bourdonův efekt) se změní poloměr střednice a zároveň dojde k deformaci příčného průřezu.